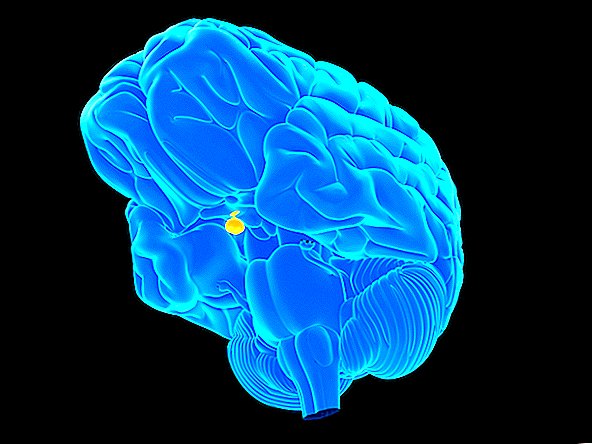
Paraksts: Mēness skats perigejā un apogejā
Es kā skolotājs vienmēr meklēju laboratorijas ar vienkāršiem studentiem piemērotiem iestatījumiem. Mana pašreizējā mīļākā ir gaismas ātruma atrašana ar šokolādi.
Jaunajā rakstā, kas nesen augšupielādēts arXiv, Kevins Krisciūns no Teksasas A&M apraksta metodi mēness orbitālas ekscentritātes noteikšanai ar pārsteidzoši zemu kļūdu, izmantojot tikai metru nūju, kartona gabalu un programmu, kas paredzēta līkņu pielāgošanai mainīgas zvaigznes.
Šī metode izmanto faktu, ka ekscentriskumu var noteikt no objekta vidējā leņķa lieluma un pusi no tā amplitūdas attiecības. Tādējādi galvenais mērķis ir izmērīt šos divus daudzumus.
Kevina stratēģija, kā to izdarīt, ir izmantot kartona novērošanas caurumu, kas var slīdēt gar metru nūju. Palūkojoties caur mēness caurumu un bīdot karti uz priekšu un atpakaļ, līdz cauruma leņķa izmērs tikai pārklājas ar mēnesi. No tā cauruma diametrs, dalīts ar attālumu lejā līdz skaitītāja nūjai, dod leņķa lielumu, pateicoties mazā leņķa formulai (? = D / D radiānos, ja D >> d).
Lai novērstu sistemātiskas kļūdas nepareizā vērtējumā, jo karti bīdāms uz priekšu, līdz bedrītes lielums sakrīt ar mēnesi, vislabāk ir tai pieiet arī no otra virziena; Nāk no iekšpuses no skaitītāja nūjas gala. Tam vajadzētu palīdzēt samazināt kļūdas, un Kevina mēģinājumā viņš atklāja, ka, to darot, viņam raksturīgais izplatījums bija ± 4 mm.
Šajā brīdī vēl ir jārēķinās ar sistemātisku kļūdu: skolēnam ir ierobežots izmērs, kas salīdzināms ar novērošanas caurumu. Tas izraisīs faktiskā leņķa lieluma nenovērtēšanu. Kā tāds ir nepieciešams korekcijas koeficients.
Lai iegūtu šo korekcijas koeficientu, Kevins novietoja 91 mm disku 10 metru attālumā (tam vajadzētu radīt disku ar tādu pašu leņķa izmēru kā mēness, skatoties no šī attāluma). Lai iegūtu vislabāko rezultātu, kartona slīdēšana ar caurumu vajadzētu jānovieto uz skaitītāja nūjas 681,3 mm attālumā, bet skolēna sistemātiskās kļūdas dēļ Kevins secināja, ka tas ir jānovieto 821 mm. Novērotā izvietojuma attiecība pret pareizo izvietojumu nodrošināja izmantoto korekcijas koeficientu Kevinu (1,205). Tas būtu jākalibrē katrai personai atsevišķi, un tas būtu atkarīgs arī no gaismas daudzuma novērošanas laikā, jo tas ietekmē arī skolēna diametru. Tomēr, pieņemot vienu korekcijas koeficientu, tiek gūti apmierinoši rezultāti.
Tas ļauj iegūt pareizi iegūtus datus, kurus pēc tam var izmantot, lai noteiktu vajadzīgos lielumus (vidējais leņķa lielums un 1/2 amplitūda). Lai tos noteiktu, Kevins izmantoja programmu, kas pazīstama kā PERDET, kas paredzēta sinusoīdu līkņu pielāgošanai mainīgo zvaigžņu svārstībām. Jebkura programma, kas varētu pielāgot šādas līknes datu punktiem, izmantojot?2 šim nolūkam būtu piemērota vai Furjē analīze.
Pēc šādām programmām, kad ir noteikts vidējais leņķa lielums un puse no amplitūdas, to attiecība nodrošina ekscentriskumu. Kevina eksperimentam viņš atrada vērtību 0,039 ± 0,006. Turklāt viņa noteiktais laika posms no perigeja līdz perigee bija 27,24 ± 0,29 dienas, kas lieliski saskan ar pieņemto vērtību 27,55 dienas.