Virtuālā realitāte var aizvest jūs uz dažām tālu vietām - kalnu virsotnēm, tālām pilsētām un pat fantastiskām spēļu pasaulēm. Mākslinieku un matemātiķu komanda tagad papildina šo sarakstu: universi, kur nepiemēro parastos ģeometrijas un fizikas noteikumus.
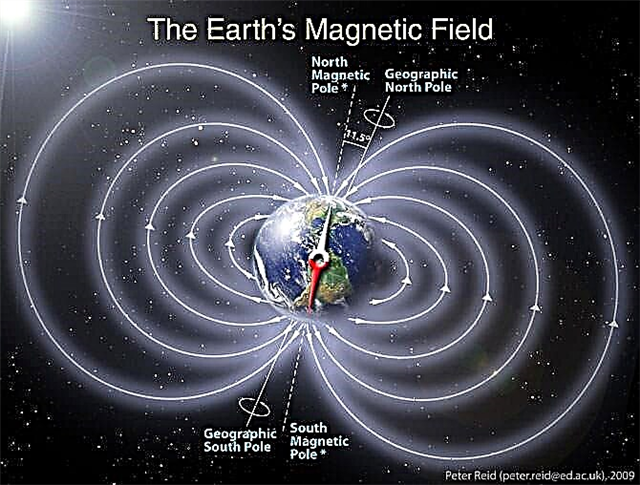
Vi Harts, kurš nodibināja pētījumu grupu eleVR, vadīja komandu, kas izveidoja virtuālu ainavu, kas izskatās kā bezgalīgi atkārtotu kameru komplekts. Šī virtuālā ainava seko tāda veida ne-Eiklīda ģeometrijas noteikumiem, ko sauc par hiperbolisko ģeometriju (sauktu arī par H-telpu). Tas darbojas savādāk nekā parastā pasaule, kas ievēro tā saukto Eiklīda ģeometriju. Šajā VR Visumā, ejot uz priekšu, grīda var nokrist no kājām, un attālumi nav tādi, kādi šķiet, viss tāpēc, ka līnijas un leņķi neuzvedas tā, kā parastajā pasaulē.
"H telpā, nedaudz paceļot galvu, tas ir normāli, bet, ja jūs veicat lielākas kustības, tas ir savādāk," tiešraidē stāstīja Henrijs Segermans, pētījumu līdzautors un Oklahomas Valsts universitātes matemātikas profesora asistents. Zinātne. Tas ir tāpēc, ka H telpā "liela daļa no tā ir ļoti tuvu jums", kas nozīmē, ka vietas daudzums starp diviem punktiem noteiktos virzienos ir mazāks nekā Eiklīda telpā, kur attāluma vienība ir nemainīgs garums.
Rezultāti ir pielietojami gan akadēmiskajā vidē, gan videospēļu nozarē. Tomēr impulss projektam bija vairāk māksla nekā zinātne: "Matemātika un māksla nav tik tālu viena no otras," sacīja Hārts. "Gan matemātikā, gan mākslā mēs varam runāt par pilnīgi izdomātām pasaulēm."
Ievērojot noteikumus
Lielākā ikdienas dzīvē izmantotā ģeometrija ir plakano telpu ģeometrija jeb Eiklīda ģeometrija, ko sauc par to, ka grieķu matemātiķis Eiklids pierakstīja daudzus principus. Piemēram, Earthlings sagaida, ka paralēlas līnijas nekad nesatiksies un ja jūs saskaitīsit trīsstūra iekšējos leņķus, tas iznāks līdz 180 grādiem. Tas nozīmē arī to, ka, ejot 10 pēdas uz priekšu, dodieties pa labi, ejiet to pašu attālumu un atkārtojiet procesu vēl trīs reizes, atgriezīsities tajā pašā punktā.
Ne-Eiklīda ģeometrija nedarbojas šādi. Trijstūrim, kas uzrakstīts uz lodes virsmas - sfēriskai ģeometriskai telpai -, tās iekšējie leņķi ir vairāk nekā 180 grādi, un trijstūrim, kas novilkts uz seglu formas virsmas - hiperboliskam ģeometriskajam telpai -, var būt mazāk grādu. Sfēriskā ģeometrija tiek izmantota navigācijā, jo Zemes virsma ir sfēriska. Hiperboliskās ģeometrijas vairāk parādās kosmoloģijā.
"Hiperboliska telpa ir drīzāk veidota kā Pringles mikroshēma," sacīja Segermans.
Rezultāts ir tāds, ka ārpus eiklidiešu pasaules izpēte, izmantojot virtuālo realitāti, būs ļoti dīvaina. Lai zinātnieki varētu pārveidot šo dīvaino karaļvalsti VR telpā, viņiem bija jāiekļauj vismaz dažas eiklīdijas funkcijas, ja tikai tā, lai tā lietotājiem būtu mazāk dezorientējoša, sacīja Segermans.
Projekts nav paredzēts tūlītējai izmantošanai. Iegūtā VR ainava varētu radīt jautras videospēļu pasaules un pat tikt izmantota, lai iemācītu studentiem orientēties šādās telpās. Turklāt šāda veida telpās varētu vizualizēt dažus datu veidus, kuros ir daudz "zarojošu koku" - kurus parasti ir sarežģīti vizualizēt.
Tas varētu būt noderīgs arī matemātikā. "Dažreiz ievadīšana šajā gadījumā ir tiešāka lieta nekā lasīšana vai aprēķināšana," sacīja Segermans. Daudziem cilvēkiem pastaigāties pa telpu, kas nav saistīta ar eiklīdiem, ir daudz vieglāk, nekā mēģināt to analizēt uz papīra, jo cilvēks ar jutekļiem mijiedarbojas tāpat kā parastā pasaulē.
Cits pētnieks, kuru viņš citē dokumentā, Džefs Vekss, piemēram, ir izveidojis lidojumu simulatorus, kas darbojas šāda veida telpās.
"" Patiesais iemesls "(vismaz manuprāt) ir ļaut cilvēkiem iegūt izpratni zarnu līmenī par dažādām ģeoklīnijām, kas nav Eiklidu valstis. Citiem vārdiem sakot, tā vietā, lai mēģinātu izprast ārpus Eiklīda esošās ģeometrijas, izmantojot formulas un abstraktus matemātiskos modeļus. , mēs vēlamies, lai cilvēki tos tieši piedzīvotu, "Liveeks savā e-pastā stāstīja neatkarīgais pētnieks Weeks, kurš ir izveidojis spēles matemātisko jēdzienu izpētei.
Mācot cilvēkiem orientēties šādās nepāra telpās, var gūt labumu no reālās pasaules arī fizikā. Piemēram, viss Visums faktiski ir kosmoss, kas nav Eiklidu apgabals, lielos kosmoloģiskos mērogos.
"Secinājums ir šāds: ja mēs vēlamies izprast dabisko pasauli, kurā mēs dzīvojam, mums jāatsakās no eiklidiešu priekšstatiem un jāapmierinās ar vairākiem citiem ģeometrijas veidiem."
Pētījums ir detalizēts divos rakstos, kas publicēti pirmsdrukas vietnē arXiv.org.